Ce qu’on va voir!

1. Introduction
2. Vocabulaire
3. La régression linéaire
4. Le “cost”
5. Le fameux Gradient Descent
6. Vectoriser les calculs (optionnel)

1. Introduction

Il est à peu près 23h et je me demande “Pourquoi je fais ça? Après tout, toutes les informations que j’écris ici sont bien mieux expliquées ailleurs sur internet!”. On ne se le cachera pas, j’ai raison.

Pourquoi, alors? Et bien, à mon avis, il y a au moins 2 avantages à ce blog.

1. En un article, on apprend des nouvelles choses, mais pas trop, et de A à Z.

Trop souvent, j’ai lu des didacticiels (tutorials #loi101) qui montrent super bien toutes les étapes de la partie apprentissage d’un algorithme, mais qui ne montre pas pantoute comment s’en servir pour faire des prédictions, c’est assez poche, si vous voulez mon avis. C’est comme si on te montrait à setter toute ta canne à pêche, comment lancer la ligne, comment la ramener, mais pas comment retirer le crochet du poisson (pire analogie? Je pense que je peux faire mieux). Ici, on va toute vouwér (malaise).

Aussi, on ne rentre pas trooppp en détails, du moins pour l’instant. Ça fait que ça reste assez accessible et rapide à lire.

1. Un sujet par semaine.

En sortant à peu près un article par semaine (so far so good), ça permet d’apprendre des nouvelles choses à chaque semaine pour des étudiants qui n’ont clairement pas le temps de suivre des longs cours en ligne (comme si moi j’avais le temps d’écrire des articles eh eh).

(pi c’est en français, tsé)

Trèves de niaisage, au boulot!

Aujourd’hui, nous allons travailler à déterminer quelle note nous devrions avoir en fonction de notre nombre d’heures d’étude (plus gros mensonge au monde).

2. Vocabulaire

L’apprentissage machine est utilisable dans plusieurs circonstances, comme on a rapidement vu la semaine passée.

Afin de clarifier un peu ce sur quoi on va travailler et de vous donner des nouveaux termes à utiliser pour impressioner vos collègues de classes, définissons dans quel contexte nous allons travailler aujourd’hui.

En apprentissage machine, on retrouve des problèmes de régression et de classification.

Problèmes de régression

Les problèmes de régression cherchent à prédire une valeur numérique. Par exemple : Le prix d’une maison, un pourcentage à un examen, le nombre d’yeux d’un poisson qui passe trop de temps dans le fleuve St-Laurent. Comme on peut facilement s’en douter, la régression linéaire travailler avec des problèmes de classification régression.

En statistiques, on retrouve des données discrètes et continues.

• Les données continues sont des données dans l’ensemble des nombres réels. Par exemple, le prix d’une maison peut être 300000$ ou 300000,05$.

• Les données discrètes sont des données de l’ensemble des nombres entiers. Par exemple, un poisson ne peut pas avoir un demi oeil.

Lorsqu’on travaille en régression, il est important de savoir avec quel genre de données on travaille pour nous aider à maximiser la performance de notre modèle.

Les problèmes de classification

Les problèmes de classification cherchent à… classifier. Par exemple : Détecter si une personne est atteinte du cancer ou non, si un objet dans une photo est un caniche ou bien si une personne est en train de sourire sur une photo. Nous reviendrons aux problèmes de classification dans le prochain article!

Dans une catégorie à part, on retrouve aussi des problèmes d’apprentissage supervisés et non-supervisés (Il existe au moins deux autres catégories dont on ne discutera pas aujourd’hui).

Problèmes supervisés

En apprentissage machine, comme j’ai rapidement expliquer dans l’article précédent, on travaille avec des exemples de données. Par exemple, dans notre problème, j’aurais besoin de savoir quelles sont les notes d’étudiants en fonction de leur nombre d’heures d’études afin d’être capable de faire des prédictions plus tard. On travaille ici en apprentissage supervisé, car nous travaillons avec des exemples pour lesquels nous avons déjà des réponses.

Problèmes non-supervisés

Dans le cas de l’apprentissage non-supervisé, nous n’avons pas les “réponses”. Imaginons, comment pourrions-nous savoir la note d’une persone qui a étudié 5 heures si nous n’avons aucune données sur le sujet?? (Hint, nous ne pouvons pas). Étant donné que les problèmes non-supervisés sont une toute autre gamme de problèmes, nous y reviendrons dans un article futur.

Nous avons défini quelques termes généraux, le reste viendra au fur et à mesure de notre lecture!

3. La régression linéaire

Si vous vous rappelez vos cours de maths du secondaire, nous voyons deux techniques de régression linéaire :

1. La droite de Mayer
2. La droite Médiane-Médiane

Aujourd’hui, nous allons voir une nouvelle technique, celle qui est utilisée en apprentissage machine!

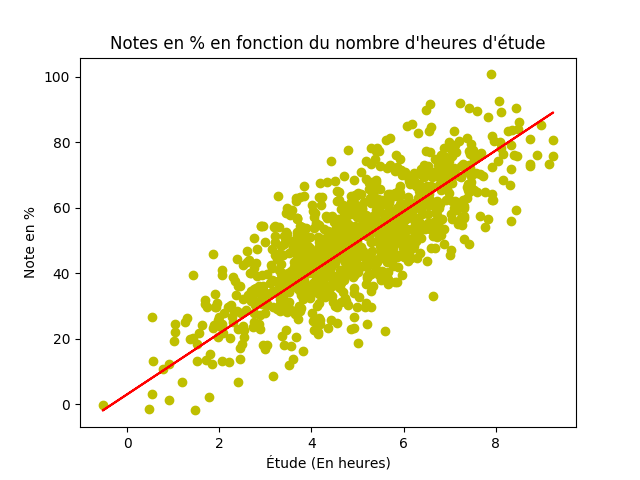
Avec la régression linéaire, on trace une droite de régression de la forme y=m*x+b qui permet d’approximer une valeur de y pour une valeur de x. Afin de trouver la meilleure droite, nous devons avoir d’autres points de référence. Dans notre cas, nous allons utiliser un exemple (fictif) de mille élèves avec leur nombre d’heures d’étude et leur note en pourcentage à un examen.

Dans notre cas, nous n’avons qu’une seule variable à considérer, le nombre d’heures d’étude. La raison pour laquelle nous n’utilisons qu’une seule valeur est que c’est beaucoup plus facile à dessiner sur un graphique et que c’est un peu moins complexe. Nous verrons dans un futur pas trop lointain comment utiliser la régression linéaire dans des situations où il y a plus d’une variable.

La génération de données

Première des choses, pour pouvoir faire de la régression, nous avons besoin de données! J’ai trouvé ici comment générer un ensemble de points en (x,y) qui ont une corrélation linéaire pas trop terrible. Vous pouvez prendre le temps d’analyser ce code, c’est pertinent, mais ce n’est pas vraiment le but de cet exercice.

def create_correlated_set(correlation):
    xx = np.array([0, 10])
    yy = np.array([0, 100])
    means = [xx.mean(), yy.mean()]
    stds = [xx.std() / 3, yy.std() / 3]

    covs = [[stds[0] ** 2, stds[0] * stds[1] * correlation],
            [stds[0] * stds[1] * correlation, stds[1] ** 2]]

    m = np.random.multivariate_normal(means, covs, 1000).T
    return np.c_[m[0], m[1]]

points = create_correlated_set(0.8)
x = points[:, 0]
y_true = points[:, 1]

L’affichage des données

En apprentissage machine, c’est pratique d’être capable de visualiser les données pour s’assurer que tout a du sens. Nous allons donc visualiser l’ensemble de données que nous venons de créer grâce à la librairie matplotlib.

import matplotlib.pyplot as plt

plt.scatter(x, y_true, color="y")
plt.xlabel("Étude (En heures)")
plt.ylabel("Note en %")
plt.title("Notes en % en fonction du nombre d'heures d'étude")
plt.show()

La fonction scatter crée une graphique avec les valeurs de x sur l’axe des x et la même chose en y. Assez simple, non?

Faire des (mauvaises) prédictions

Jusqu’à présent, nous avons généré un ensemble de données. C’est-à-dire, des valeurs de X et des valeurs de Y associés.

Il serait temps d’essayer de faire des prédictions! Si on revient à ce qui était dit tantôt, on peut faire des prédictions avec une droite de régression de la forme y=m*x+b. Et bien, nous avons le x, mais nous n’avons toujours pas de m ni de b! Mais nous ne savons toujours pas quoi utiliser comme valeurs pour obtenir un résultat optimal… Et bien, en cas d’absence d’informations, commencons avec les valeurs les plus simples possibles.

m = 1
b = 0

Va-t-on obtenir de bonnes prédictions avec cela? Certainement pas! Mais il faut bien commencer quelque part.

Essayons, qui sait. Tant qu’à y être, affichons aussi le résultat!

y_pred = m*x + b
plt.scatter(x, y_pred, color="y")
plt.xlabel("Étude (En heures)")
plt.ylabel("Note en %")
plt.title("Notes en % en fonction du nombre d'heures d'étude")
plt.show()

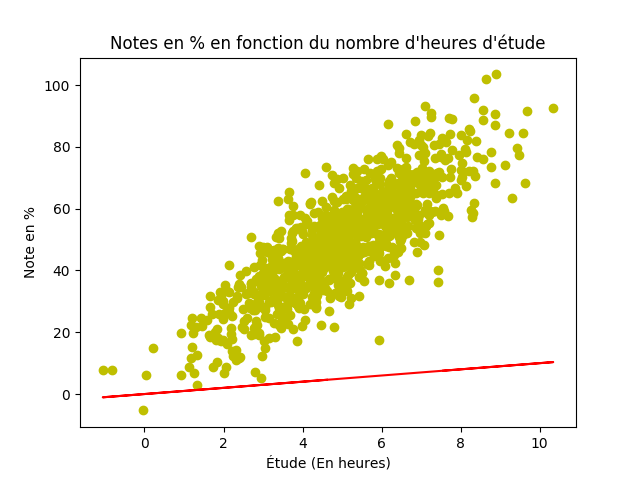
Isshhh… On ira pas loin avec ça!

Regardons, voir, à quel point est-ce que nous sommes loin d’une réponse valable.

print("La valeur attendue pour x=", x[4], " est ", y_true[4])
print("La valeur obtenue est : ", y_pred[4])

Attention, les valeurs de x et y sont complètement aléatoires, donc c’est bien possibles que vous n’obteniez pas la même chose que moi.

Si on regarde le résultat :

La valeur attendue pour x= 5.87932122884 est 45.871013863 La valeur obtenue est : 5.87932122884

Ce n’est pas très beau.

Comment pouvons nous choisir de meilleures valeurs pour m et b? Prochaine étape!!

4. Le “cost”

En apprentissage machine, on définit le coût d’une fonction comme étant l’erreur d’approximation de la fonction. Plus le coût est haut, plus la fonction est “dans l’champ”.

Comment pourrait-on définir cette fonction? On pourrait le faire de plusieurs façons en fait. Il existe plusieurs manières de défininr l’erreur d’une fonction, mais nous en discuterons plus en détail dans un futur quelconque (pas tout de suite en tout cas!).

Dans notre cas, nous allons utiliser le Mean Square Error. Ce que le MSE calcule, c’est la distance entre chaque prédictions par rapport à sa valeur réelle au carré, puis on fait une moyenne. Pourquoi au carré? Bonne question! L’erreur est au carré pour que les erreurs très grandes aient un impact encore plus grand sur l’erreur et que nous n’ayons pas à nous soucier des valeurs négatives si la prédiction est plus grande que la valeur réelle. La dernière raison est surement la plus importante : Le MSE se dérive facilement (Attention, MAT145)! On va voir pourquoi c’est si important dans la prochaine section.

Mathématiquement parlant, ça va comme suit :

\(MSE = \frac{1}{n} * \sum{(y_{true} - y_{pred})^2}\) où n représente le nombre de données dans l’ensemble de test.

Maintenant, en code !

def compute_cost(y_pred, y_true):
    cost = 0.0

    for true, pred in zip(y_true, y_pred):
        cost += (true - pred)**2

    return cost / len(y_pred)

print(compute_cost(y_pred, y_true))

Dans mon cas, l’erreur tourne autour de : 2156.68763664 D’ici la fin, ça devrait tourner plus autour de 100. On a du travail à faire!

5. Le fameux Gradient Descent

Si vous avez déjà lu ne serait-ce qu’un article sur l’apprentissage machine, vous avez sûrement lu “Gradient Descent”, sans nécessairement savoir qu’est-ce que ça fait.

Tout change maintenant!

On se rappelle la section précédente : Nous avons une fonction que nous cherchons à minimiser. Peut-être avez-vous vu dans vos cours de mathématiques comment faire pour minimiser une fonction. Toutefois, on peut avoir à faire ici à des fonctions assez “funky”, excusez-moi l’expression, donc les techniques traditionnelles ne fonctionneront pas toujours très bien!

Dans le MSE, on retrouve deux variables : m et b.

Si je dérives le MSE en fonction de m (lire ici dérivation partielle) et que la dérivée au points m était négative. Ça veut donc dire que si j’augmentais un peu ma valeur de m, probablement que le cout (le MSE) diminuerait! Si je faisais la même chose en b et que ma dérivée du MSE au point b était positive, par exemple, alors si je diminue ma valeur de b, il y a de bonnes chances que le MSE diminue aussi.

En gros, en utilisant des dérivées partielles, on peut réduire petit à petit le coût de notre algorithme d’apprentissage, qui est représenté par le MSE.

Entre en scène le gradient descent (excusez moi, je ne sais pas vraiment ce que c’est en français. La descente graduée? La gradation descendante? Who knows?!?).

Le gradient descent, c’est exactement ce que nous venons de voir.

• Prendre la fonction qui définit notre cout (le MSE)
• Dériver la fonction selon chacun de nos paramètres (m et b)
• Calculer la dérivée au point m et b actuels (m=1 et b=0 dans notre cas)
• Ajuster nos paramètres en fonction des nouvelles dérivées.

Pour ne pas se casser la tête, voici les dérivées en m et b du MSE, j’vous les donne, gratisse :

\(\frac{\delta MSE}{\delta m} = \frac{1}{n} * \sum{2 * x * (y_{pred} - y_{true})}\)

et

\(\frac{\delta MSE}{\delta b} = \frac{1}{n} * \sum{2 * (y_{pred} - y_{true})}\)

C’est quasiment trop facilement! On peut peut-être se demander d’où vient le x dans la dérivée en m, non? Et bien, si on prend r’garde ça de plus près, on se rappelle que y_pred=m*x + b. Si on remplace y_pred par l’équation de droite dans l’équation du MSE, tout devient logique (du moins, si vous connaissez votre calcul différentiel). Sachez que vous n’avez pas à dériver des équations mathématiques directement dans votre code, ce serait bien trop complexe. Vous pouvez facilement faire les dérivées par vous-même avant (ou aller voir sur Internet).

Maintenant, avec du code!

def compute_gradients(x, y_pred, y_true):
  grad_m = 0
  grad_b = 0

  for one_x, true, pred in zip(x, y_true, y_pred):
      grad_m += 2*one_x*(pred - true)
      grad_b += 2 * (pred - true)

  return grad_m / len(x), grad_b / len(x)

“Pretty much” ce qu’on vient de voir, non?

Voyons voir ce que ça donne, ces calculs là, avec nos données aléatoires! (J’ai fait une erreur, je dois l’avouer. J’ai rouler différents bouts d’exercices avec différents ensembles de données aléatoires, donc les chiffres ne se suivent pas tant. Mais ce n’est pas suuppeerr grave. En fait, si je ne l’avais pas dit surement que vous ne vous en seriez pas rendu compte!)

m_grad, b_grad = compute_gradients(x,y_pred,y_true)

print(m_grad)
print(b_grad)

Sort ceci :

m_grad = 494.632724488 b_grad = 90.3160958761

Là, on jase, mais ma valeur de m en ce moment est de un. Si j’ajoutais 494, surement que je n’aiderais pas la situation.

On ajoute un autre paramètre, le learning_rate. Le learning rate sert à réduire l’impact des dérivées. Quelle est la meilleure valeur pour le learning rate? Bonne question! On ne le sait pas. C’est toujours un peu aléatoire et il faut en essayer plusieurs pour essayer de trouver la meilleure valeur possible. C’est en fait ce qu’on appelle un hyper parameter (on y reviendra).

Dans notre cas, j’ai essayé quelques valeurs et j’ai trouvé que 0.0005 n’était pas trop terrible. Mais je vous conseille gros comme le monde de downloader le code de ce blog sur GitHub (le lien sera à la fin de l’article) et d’essayer différentes valeurs.

Donc, on l’utilise ainsi :

m -= learning_rate*grad_m
b -= learning_rate*grad_b

Pourquoi est-ce que ces valeurs sont soustraites? C’est que, comme je disais tantôt, si la dérivée est positive, je voudrais diminuer ma valeur, si la dérivée est négative, on voudra l’augmenter. Le moins vient permettre ça. Si ça ne semble pas clair, prenez le temps d’y réfléchir un peu plus!

Là, je veux vous encourager, on achève!

Il ne reste qu’une seule étape. Faire le gradient descent une seule fois ne nous aidera pas. Ce n’est tout simplement pas suffisant pour ajuster notre courbe.

On va donc répéter l’étape du gradient descent plein de fois!!! C’est ce qu’on appelle le e_poch. Je ne sais pas vraiment pourquoi.

Voilà donc, le reste du code. Comprenant le calcul des gradients, l’ajustement de m et b et, pour la luck, on “print” la valeur du cost à chaque fois. Pour bien montrer que ça fonctionne, ce qu’on fait.

n_epoch = 400
for step in range(0, n_epoch):

    grad_m, grad_b = compute_gradients(x, y_pred, y_true)

    m += learning_rate*grad_m
    b += learning_rate*grad_b

    y_pred = m * x + b

    cost = compute_cost(y_pred, y_true)

    if step % 100 == 0:
        print("Step ", step, " : cost = ", cost)
        plot_everything(x, y_pred, y_true)

n_epoch est aussi un “genre” de hyper parameter parce que plus on le met haut, plus notre algorithme devrait bien performer, mais plus ce sera long à faire. Et à un point, et bien la différence de performance n’en vaut plus la peine, tout simplement.

Qu’est-ce qu’on obtient, à la fin de tout ça? (On regarde la ligne rouge ici)

(Oui oui, j’ai réutiliser la même image qu’au début. Aucuns regrets.)

Tout le code est ici (J’ai volontairement laissé la partie “Faire de nouvelles prédictions” de côté, parce que c’est que quelques lignes de code et que ça va vous “forcer” à aller voir sur Git pour apprendre des p’tites affaires #clickbait). De plus, je vous encourage à essayer de modifier des trucs, pour bien comprendre comment tout fonctionne.

Bonne chance :)

6. Vectoriser les calculs (optionnel)

C’est optionnel, mais pas tant.

Remarquez que pour calculer le coût et le gradient descent, on a utiliser des boucles for.

Et bien, vous vous imaginerez bien que si j’avais 200000 exemples à 400 epoch, j’aurais donc 80 millions d’itérations à faire pour calculer le cout et les gradients. Long longtemps, comme on dit.

On pourrait paralléliser tous les calculs, mais il y a encore mieux à faire!

Python permet d’exploiter des libraires écrites en C (spécialement compilées) comme si ne rien n’était. C’est le cas de la librairie numpy. Si vous observez le code de create_correlated_set, on s’en sert déjà!

numpy permet de faire des calculs en parallèles et en C, qui est évidemment plus rapide qu’en Python. Bref, c’est une librairie qui fera beaucoup plus rapidement les choses que vous et moi. Ça permet de travailler avec des array comme si c’était des matrices (parce qu’en quelques sortes, ce l’etsest).

Je vous invite à explorer d’avantage cette librairie, parce qu’elle est très importante, mais je n’entrerai pas dans les détails maintenant.

En gros,

cost = 0.0

for true, pred in zip(y_true, y_pred):
    cost += (true - pred)**2

return cost / len(y_pred)

# Devient

return np.sum(np.power(y_true - y_pred, 2), axis=0, keepdims=True) / len(y_pred)

et

grad_m = 0
grad_b = 0

for one_x, true, pred in zip(x, y_true, y_pred):
    grad_m += -2*one_x*(pred - true)
    grad_b += -2 * (pred - true)

return grad_m  / len(x), grad_b  / len(x)

# Devient
grad_m = np.sum(-2 * x * (y_pred - y_true), axis=0, keepdims=True) / x.shape[0]
grad_b = np.sum(-2*(y_pred - y_true), axis=0, keepdims=True) / x.shape[0]

Mais en beaucoup plus rapide et concis. En plus, ça ressemble pas mal plus à des expressions mathématiques.